Articulation Point (Cut Point) & Bridge

3 minutes read

Articulation Point & Bridge

31/07/2019

I. Definition

Ta xét trong undirected graph.

  • Articulation Point (đỉnh khớp): Là đỉnh mà nếu cắt bỏ đi sẽ làm disconnect graph (trong connected graph) còn đối với disconnected graph thì nó làm tăng số connected component.
  • Bridge: Là cạnh mà nếu bỏ đi … (giống khớp)

II. Finding Articulation Point

1. Thuật toán tầm thường

Với mỗi đỉnh trong graph, ta thử cắt bỏ đi và đếm số thành phần liên thông. Nếu tăng thì đỉnh đó là khớp, ngược lại thì không. Gắn đỉnh đó lại và thử bỏ đỉnh khác cho đến khi ta thử hết các đỉnh của graph.
$$ \Rightarrow O(V*O(DFS)) = O(V(V+E))$$

2. Thuật toán cải tiến (Tarjan)

Tận dụng sức mạnh của DFS.
Nhắc lại, các loại edges trong 1 tree.

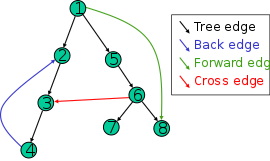
tree_edges

Trong DFS Tree, chỉ có Back Edges và Tree Edges.

Xét 1 đỉnh $u$ trong đồ thị:

  • Nếu $u$ là root và $u$ có 2 con trở lên $\Rightarrow u$ là khớp
  • Nếu $u$ khác root và subtree rooted at v (children of u) has NOT back edge to ancestor of u $\Rightarrow u$ là khớp.

Minh họa:

AP_minhhoa

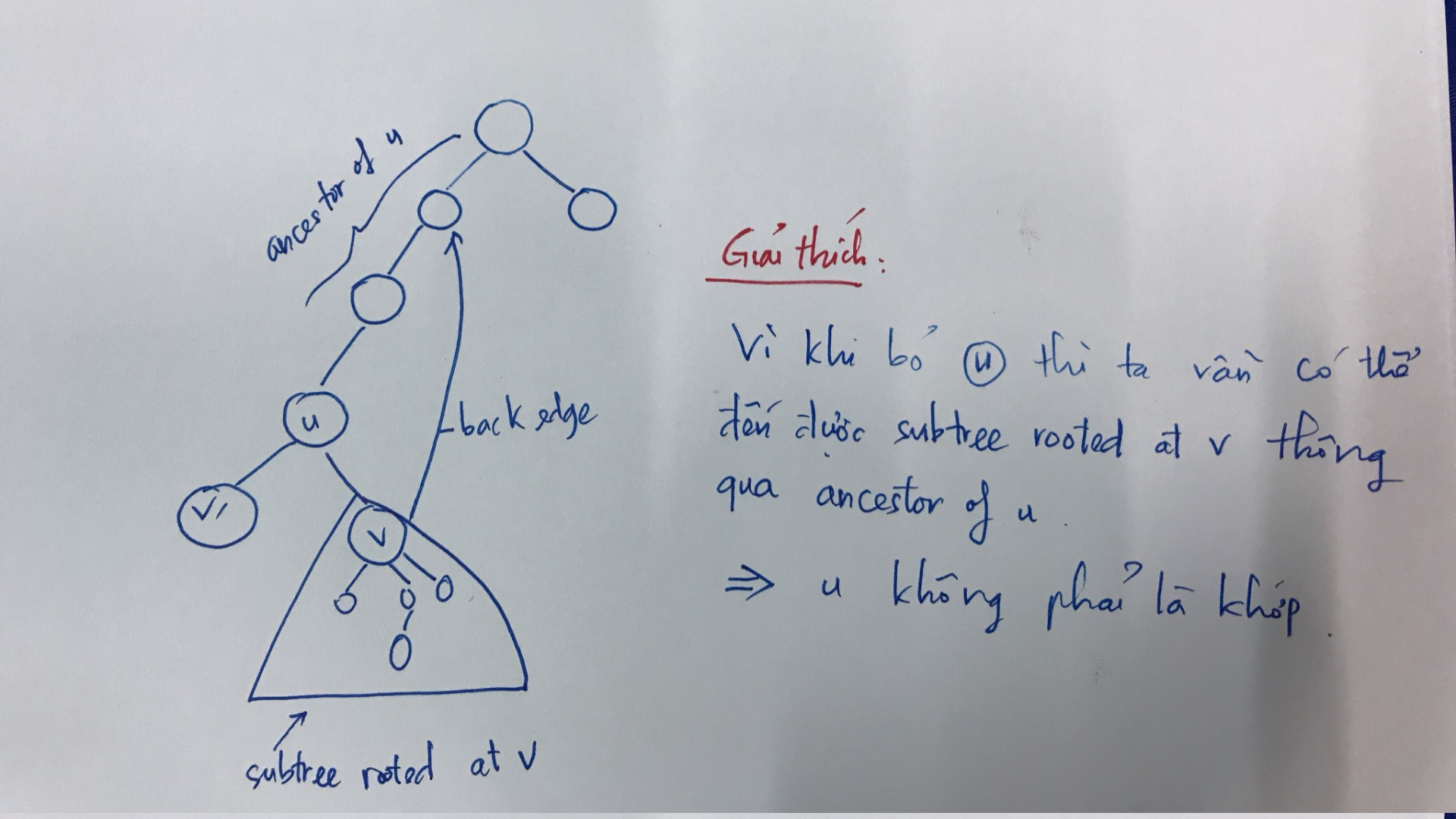
Nếu không có back edge thì khi bỏ $u$ sẽ diconnect graph với subtree rooted at v. $\Rightarrow u$ là khớp.

3. Implementation

Làm thế nào để ta biết được 1 đỉnh $u$ có phải là khớp hay không?

  • Đối với trường hợp $u$ là root: ta cứ đếm số con tại mỗi node, nếu $u$ là root và có $>=2$ con thì $u$ là khớp.
  • Trường hợp 2 ta lưu thêm:
    • $disc[u]$: thời gian khám phá ra đỉnh $u$ (discovery)
    • $low[u]$: $min(disc[u], disc[w])$, trong đó $w$ is ancestor of u and there is a back edge from some descendant of $u$ to $w$. Tức là ta lưu lại số thứ tự của node sớm nhất (có thể = cha $u$ nhưng theo con đường back edge của đám con cháu) mà từ đó có thể đi tới cây con rooted at $u$ (include $u$)

    Thì khi $low[v] \geq disc[u]$ chứng tỏ $u$ là AP ($"="$ khi back edge của con $v$ nó trỏ ngay $u$)

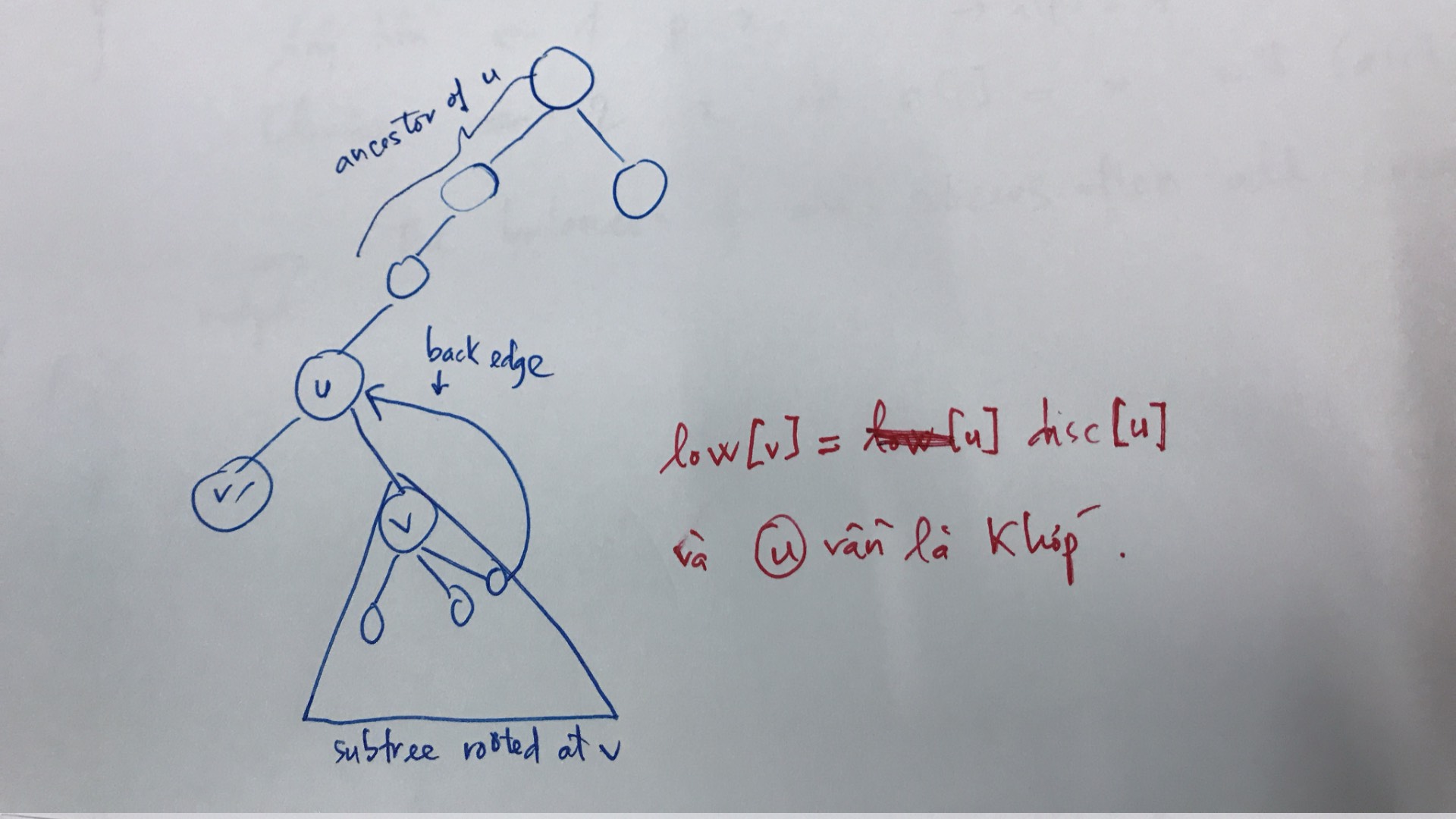
lowv_equal_discu

$\Rightarrow $Code: Tao xin copy nguyên source trên trang cp-algorithm bởi vì nó code quá tuyệt vời.
$tin$ = $disc$ (time into node).

 1const int N = 1e5; //maximum number of vertices
 2int n; //number of nodes
 3vector<vector<int>> g;
 4bool vis[N] = {0}, cutPoint[N] = {0};
 5int tin[N], low[N], timer = 0;
 6
 7void dfs(int v, int p = -1){
 8    vis[v] = true;
 9    tin[v] = low[v] = timer++;
10    int child = 0;
11    for(auto to : g[v]){
12        if (to == p) continue;
13        if (!vis[to]){
14            child++;
15            dfs(to, v);
16            low[v] = min(low[v], low[to]);
17            if (low[to] >= tin[v] && p != -1)
18                cutPoint[v] = true; //có trùng
19        } else {
20            low[v] = min(low[v], tin[to]);
21        }
22    }
23    if (p == -1 & child > 1) 
24        cutPoint[v] = true;
25}
26void find_cutpoints(){
27    timer = 0;
28    memset(vis, 0, sizeof vis);
29    memset(cutPoint, 0, sizeof cutPoint);
30    for (int i=0; i<n; i++)
31        if(!vis[i]) dfs(i);
32}

III. Finding Bridges

Hoàn toàn tương tự, chỉ khác ở điều kiện: $low[v] > disc[u]$ thay vì $low[v] \geq disc[u]$ và không có chuyện trùng nhau.

1bridge.push_back({a, b}); //ko co trung

IV. Tham khảo