Binary Indexed Tree (Fenwick Tree)

24/06/2019

Định nghĩa:

Fenwick Tree (Binary Indexed Tree) là một CTDL với n node (n+1 nodes với node gốc bù nhìn) chứa thông tin (thường là tổng cộng dồn) về các phần tử trong đoạn (i-(i&-i), i] (mảng tính từ $1$)

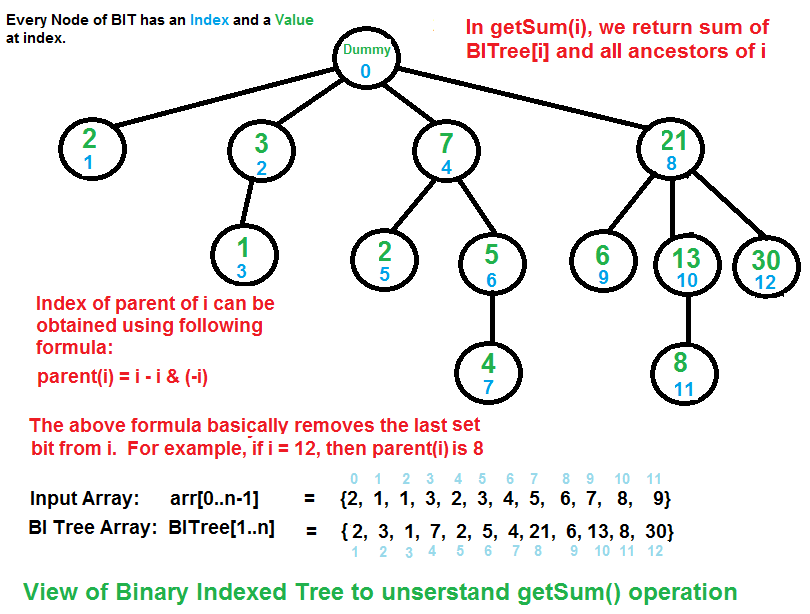
• Nhận xét: Cây getSum vs cây Update khác nhau:
  • in GetSum: parent(i) = i-(i&-i)
  • in Update: parent(i) = i+(i&-i)

Mục đích:

Mục đích cây này là để tính range sum và khi update 1 phần tử trong mảng a thì các range sum involved cũng được update với chi phí thấp.
=> Chi phí tính range sum & update value đều là O(log n)

Thao tác

1. Khởi tạo fenwick[n+1]

• Khởi tạo tất cả fen[i] = 0
  fen[n+1]={0}
• Coi như ta đang update các phần tử của mảng, a[i] (i in [1..n]) và update vào fen[i] & các parent of (i)
  ** parent(i) = i+ (i&-i)

1  void update (int pos, int val){
2      while(pos<=n){
3          fen[pos]+=val;
4          pos+= (pos&-pos);
5      }
6  }

• Bàn về update: Khi update a[i], ta phải update những fen[j] với range (j-(j&-j), j] contains i Nghĩa là: j = i + bit 1 (ở 1 vị trí nào đó) đảm bảo biên phải luôn > i \
  Biên trái:
  • Nếu add bit 1 vào trước LSOne(i) thì khi j - (j&-j)+ 1 > i (không chứa i) –> Loại
  • Nếu add bit 1 ngay tại LSOne(i): thì j - (j&-j)+1 luôn >=i (contains i) –> Chọn Chỉ có ở đây là lượng thêm vào ít hơn lượng bớt ra nên nó contains i
  • Nếu add bit 1 vào sau LSOne(i) Thì j - (j&-j) + 1 > i cũng ko contains i, lượng thêm vào nó nhiều hơn lương bớt ra

Chú thích: LSOne(i) là giá trị bit 1 trái nhất của i. (Least Significant bit)
Củ chuối vl, đọc giải thích + implement trong Handbook ok hơn!!!

2. Get prefix sum

1    int sum (int pos){ //sum all [1..pos]
2        int ans = 0;
3        while(pos > 0){
4            ans += fen[pos];
5            pos -= (pos&-pos);
6        }
7    }

Từ đây ta có thể tính sum(int l, int r) = sum(r) - sum(l-1)