Greatest Common Divisor using Euclidean Algorithm

11/07/2019

I. Implementation

1typedef long long ll;
2ll gcd (ll a, ll b){
3    return b==0? a : gcd(b, a%b); //phải hỏi b==0? chứ b=0 thì làm sao a chia dư 0 được.
4}

II. Interpretation

Thuật toán Euclid tìm ước chung lớn nhất giữa 2 số $a, b$.
Không mất tính tổng quát, giả sử $a > b$.

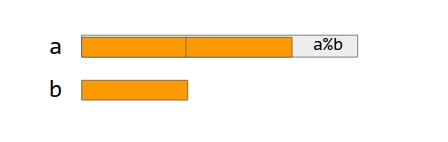
Nhìn hình, ta thấy, $gcd(a, b) = x$ khi và chỉ khi $x$ là ước của $a$, $x$ cũng là ước của $b$ và $x$ lớn nhất.

Mà $$\begin{cases}a = nb + (a \% b) \\a \% x = 0 \ \wedge b \% x = 0 \Rightarrow nb \% x = 0 \end{cases}$$

Nên $$ (a\%b)\ \%x = 0$$.
Suy ra: $$gcd(a, b) = gcd(b, a\% b)$$ $$(=x)$$

Corner Case (final recurrence)

• $ a = 0 $ hoặc $ b = 0 $ thì $\ gcd(a , b) =$ thằng còn lại khác $0$.
• $ a = 0 $ và $ b = 0 $ thì $\ gcd(0, 0) = 0$ (casio 570VN Plus).
  $\Rightarrow $ Cách cài đặt rất đúng.