Graph Traversal

12/09/2019

We discuss about the way we traverse a graph or a tree.
Assuming we are using adjacent list to represent a graph.

I. Depth-First Search (DFS)

Idea: Đi sâu rồi quần lại.

1. Implement

 1vector<int> g[N]; //or vector<vector<int>> g;
 2bool vis[N];
 3void dfs(int v){  //vertex
 4    vis[v] = true;
 5    for(auto u:g[v]){  //always for u =))
 6        if (!vis[u]) dfs(u);
 7    }
 8}
 9//in main
10for(int i=0; i<n; i++){
11    if (!vis[i]) dfs(i);
12}

Complexity: $$\Rightarrow O(V+E)$$.

2. Application

2.1. Connectivity Check, Count #CC

Một đồ thị là connected nếu nó chỉ có 1 CC (connected component). So, giống như việc đếm số CC, nếu số CC > 1 thì đồ thị là không kết nối.

1    dfs(0);
2    for(int i=0; i<n; i++){
3        if (!vis[i]) {
4            cout << "Unconnected Graph";
5            return 0;
6        }
7    }
8    cout << "Connected Graph";

2.2. Finding Cycles

Nếu trong quá trình duyệt graph mà phát hiện một đỉnh đã visited mà không phải cha nó (theo chiều đang duyệt) thì chứng tỏ nó có cycle.

 1vector<int> g[N];
 2bool vis[N];
 3bool dfs(int v, int p = -1){
 4    vis[v] = true;
 5    for(auto u:g[v]){
 6        if (!vis){
 7            if (dfs(u, v)) return true;
 8        } else {
 9            if (u != p) return true;
10        }
11    }
12    return false;
13}
14//in main
15for(int i=0; i<n; i++){
16    if (!vis[i]) if(dfs(i)) cout << "Cycle", break;
17}
18cout << "No cycles";

2.3. Bipartiteness Check

Có thể color graph với chỉ 2 màu? Ý tưởng: sơn nó màu Blue thì các đỉnh kề nó phải màu Red, cứ thế nếu phát hiện thằng nào đã sơn và cùng màu thì fail check.
Thiết nghĩ nên tham khảo: cp-algorithms, một bài viết quá ngon.

II. Breath-First Search (BFS)

Idea: Lan truyền theo chiều rộng Một điểm khác biệt của BFS vs DFS là nó có thể tìm đường đi ngắn nhất khi mà cost giữa tất cả các cạnh như nhau.

1. Implement

 1bool vis[N];
 2vector<int> g[N];
 3void bfs(int s){  //start vertex
 4    queue<int> q;
 5    vis[s] = true;
 6    q.push(s);
 7    while(!q.empty()){
 8        int v = q.front(); p.pop();  //vertex
 9        for(auto u: g[v]){  //always u in g[v]
10            if (!vis[u]){
11                vis[u] = true;
12                q.push(u);
13            }
14        }
15    }
16}
17
18//in main
19for(int i=0; i<n; i++){
20    if (!vis[i]) bfs(i);
21}

Complexity: $$\Rightarrow O(V+E)$$.

2. Application

III. Why BFS & DSF has complexity $O(V+E)$?

Vì ta lưu đồ thị ở dạng adjacent list.
Mỗi thao tác duyệt qua cạnh và đỉnh là $O(1)$.
$O(V+E)$ thực chất là cộng vật lý luôn á. Nhưng mà trong asymtomic complexity người ta nói $O(x+y) = O(max(x,y))$ vì $O(x+y) \leq O(2*max(x,y)) = O(max(x,y))$ ta bỏ đi hằng số $2$ as usual.
Xét đồ thị:

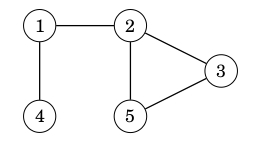
Khi lưu trong máy tính sẽ là mảng $g$ các vector.

1g[1] = {2, 4}  
2g[2] = {1, 3, 5}  
3g[3] = {2, 5}  
4g[4] = {1}  
5g[5] = {2, 3}  

Ta xét BFS, giả sử xuất phát ta gọi $\rightarrow$ BFS(1):
Duyệt qua tất cả 2 các phần tử trong g[1]: $2 = g[1].size()$
$\rightarrow$ BFS(2): duyệt qua 3 phần tử trong g[2]: $3 = g[2].size()$
$\rightarrow$ BFS(4): duyệt qua 1 phần tử trong g[4]: $1 = g[4].size()$
$\rightarrow$ BFS(3): duyệt qua 2 phần tử trong g[3]: $2 = g[3].size()$
$\rightarrow$ BFS(5): duyệt qua 2 phần tử trong g[5]: $2 = g[5].size()$

Thao tác nó tới đỉnh $i$ là $O(1)$, giống như ta duyệt qua các adjacent list, ta đến từng đỉnh, dù nó có cô độc thì cũng đã đến rồi, chi phí vẫn là $O(1)$, so:

• Duyệt qua từng đỉnh mất $O(n) = O(V)$.
• Tại mỗi đỉnh $i$ nó duyệt qua $g[i].size()$ các đỉnh kề.
  Để ý sẽ thấy, $g[i].size() = deg(i)$ (số cạnh connect với i).

$$\Rightarrow O(\sum_{i=1}^{n} deg(i)) = O(2E)$$.
Vậy complexity chính xác là: $O(V+2E)$.

Tham khảo: CP handbook, cp-algorithms.