KMP Algorithm
Knuth-Morris-Pratt algorithm
10/07/2019
I. Bài toán:
Cho chuỗi Text $T$ (length = $n$) và Pattern $P$ (length = $m$). Tìm số lần xuất hiện của $P$ trong $T$.
$\Rightarrow$ Naive Solution:
Tại mỗi vị trí $i$ trong $T$, ta so sánh nó với $P$.
code chơi thôi:
1int cnt = 0;
2for (int i = 0; i <= n-m; i++){
3 bool is_match = true;
4 for (int j = 0; j < m; j++){
5 if (P[j] == T[i+j]) continue;
6 is_match = false;
7 break;
8 }
9 if (is_match) cnt++;
10}
$$\Rightarrow O(n*m) $$
II. Ý tưởng của KMP
Nhược điểm của Naive Algorithm:
Xét ví dụ:
$T = ‘AAAABBA’$
$P = ‘AAAA’$
Thì khi $i$ chạy tới $3$ $(AAAA)$ thì được 1 lần count $(cnt = 1)$ nhưng sau đó nó phải so sánh lại từ $i=1$ với $P$.
Xem rõ ở link: https://www.geeksforgeeks.org/kmp-algorithm-for-pattern-searching/
KMP ra đời!!!
Giúp giảm độ phức tạp còn $O(n)$.
Sở dĩ độ phức tạp còn $O(n)$ vì KMP luôn hướng con trỏ $i$ trong $T$ đi về phía trước và không quay lui.
HOW DOES KMP WORK?
Giả sử quá trình đang ở trạng thái:
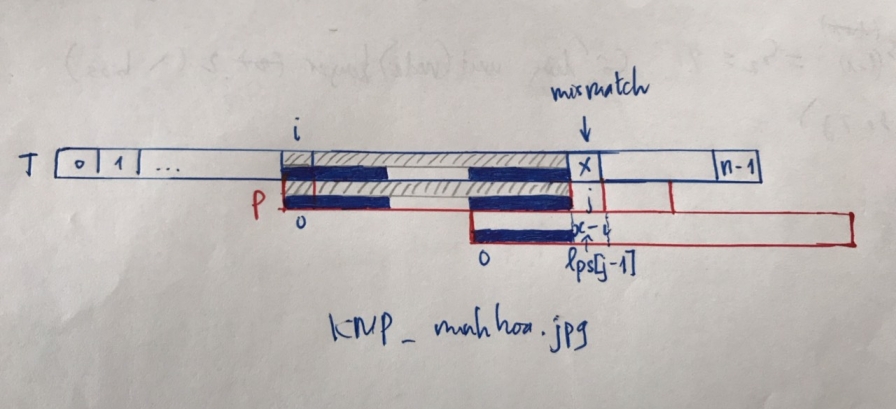
Ta gặp mismatch tại vị trí $x$, làm sao để không quay lui con trỏ mà vẫn tìm được các $P$ trong $T$?.
Ta có nhận xét:
- Đoạn $T[i:x-1] = P[0:x-i-1]$
- $P$ không thể xuất hiện tại $i$, $P$ có thể xuất hiện tại $i+1$, $i+2$, … . Trong đoạn ta đang quan tâm, $P$ chỉ có thể xuất hiện tại vị trí $j$ (i < j < x) khi và chỉ khi đoạn $T[j:x-1]$ là tiền tố của $P$. Bởi nếu một đoạn $T[j:x-1]$ bất kì mà không phải là tiền tố của $T$ thì so sánh thêm $T[x]$ có ý nghĩa gì đâu.
Vậy ta phải tìm được là khi mismatch (or xong pattern) thì ta sẽ trượt $P$ đến đâu để so sánh tiếp với $T[x]$. $P$ phải trượt đến khi nó trùng với một hậu tố của $T[i:x-1]$ (dài nhất nhé).
Xây dựng mảng trượt:
Vì đoạn $T[i:x-1]$ bao giờ cũng $= P[0:x-1]$ nên ta chỉ cần xây dựng bảng
$lps[i], \forall i \in [0:m-1]$ (longest prefix suffix) là nó phủ sóng hết tất cả các trường hợp có thể có của $T[i:x-1]$.
III. Implement
1. Xây dựng bảng lps[i]
1int* compute_LPS_array(string P){
2 int m = P.length();
3 int lps[m];
4 lps[0] = 0;
5 int len = 0;
6 int i = 1;
7 while (i < m) {
8 if (P[i] == P[len]) {
9 len++;
10 lps[i] = len;
11 i++;
12 } else{
13 if (len != 0){
14 len = lps[len - 1];
15 } else {
16 lps[i] = 0;
17 i++;
18 }
19 }
20 }
21 return lps;
22}
$$\Rightarrow O(m)$$
Giải thích:
Mày đang ở vị trí $i$, đi tính $lps[i]$.
Thì mày đã có $lps[i-1] =$ chiều dài dãy con dài nhất vừa là prefix, vừa là suffix của chuỗi $P[:i-1]$.
Thì khi thêm kí tự $P[i]$ vào, chuỗi con dài nhất nó có thể đạt tới là $lps[i-1] + 1$ khi và chỉ khi $P[i] = P[lps[i-1]]$; (trong code là $P[len]$, vì theo thứ tự nên len chính là $lps[i-1]$).
Nhưng nếu $P[i] != P[lps[i-1]]$ thì sao, thì có nghĩa là tìm chuỗi con khác vừa là tiền tố vừa là hậu tố của $P[:i]$ (chắc chắn là ngắn hơn len + 1 rồi).
Chuỗi con này tìm như thế nào?
Có phải là vì $lps[i-1] = len$ nên $P[0:len-1] = P[i-len:i-1]$ cho nên chuỗi $lps[i]$ có thể có là $lps[len-1] + 1$ nếu $P[lps[len-1]] == P[i]$. Cứ như vậy thôi.
Hình vẽ minh họa:
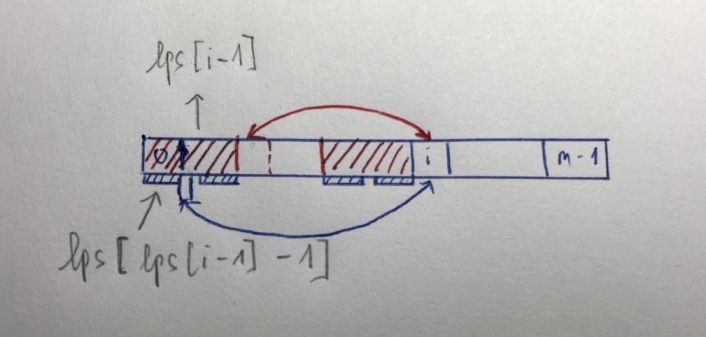
2. KMP Search
1void KMPSearch(string P, string T){
2 int m = P.length();
3 int n = T.length();
4 int* lps = compute_LPS_array(P);
5 int i = 0; //index for T
6 int j = 0; //index for P
7 while (i < n){
8 if (P[j] == T[i]) {
9 j++;
10 i++;
11 }
12 if (j == m){
13 cout << "Found pattern at index " << i-j << endl;
14 j = lps[j-1];
15 }
16 else if (i < n && P[j] != T[i]){
17 if (j != 0)
18 j = lps[j-1];
19 else
20 i = i + 1;
21 }
22 }
23}
$$\Rightarrow O(n)$$