Polist Notation

29/06/2019

I. Kí pháp Balan là gì? (What is Polish Notation)

Kí pháp Balan là một dạng viết khác của biểu thức toán học.

• Balan tiền tố (prefix): Đưa các toán tử lên đầu
• Balan ngược: Đưa các toán tử ra sau cùng

Trong kí pháp Balan, các dấu ngoặc bị lược bỏ
Ví dụ: Xét biểu thức: $3 + 5*(6-3) + 1$

• Balan: $ + + 3 * 5 - 6\ 3\ 1$
• Balan ngược: $3\ 5\ 6\ 3 - * + 1 +$

Để xây dựng được kí pháp Balan, ta dùng cây biểu thức:

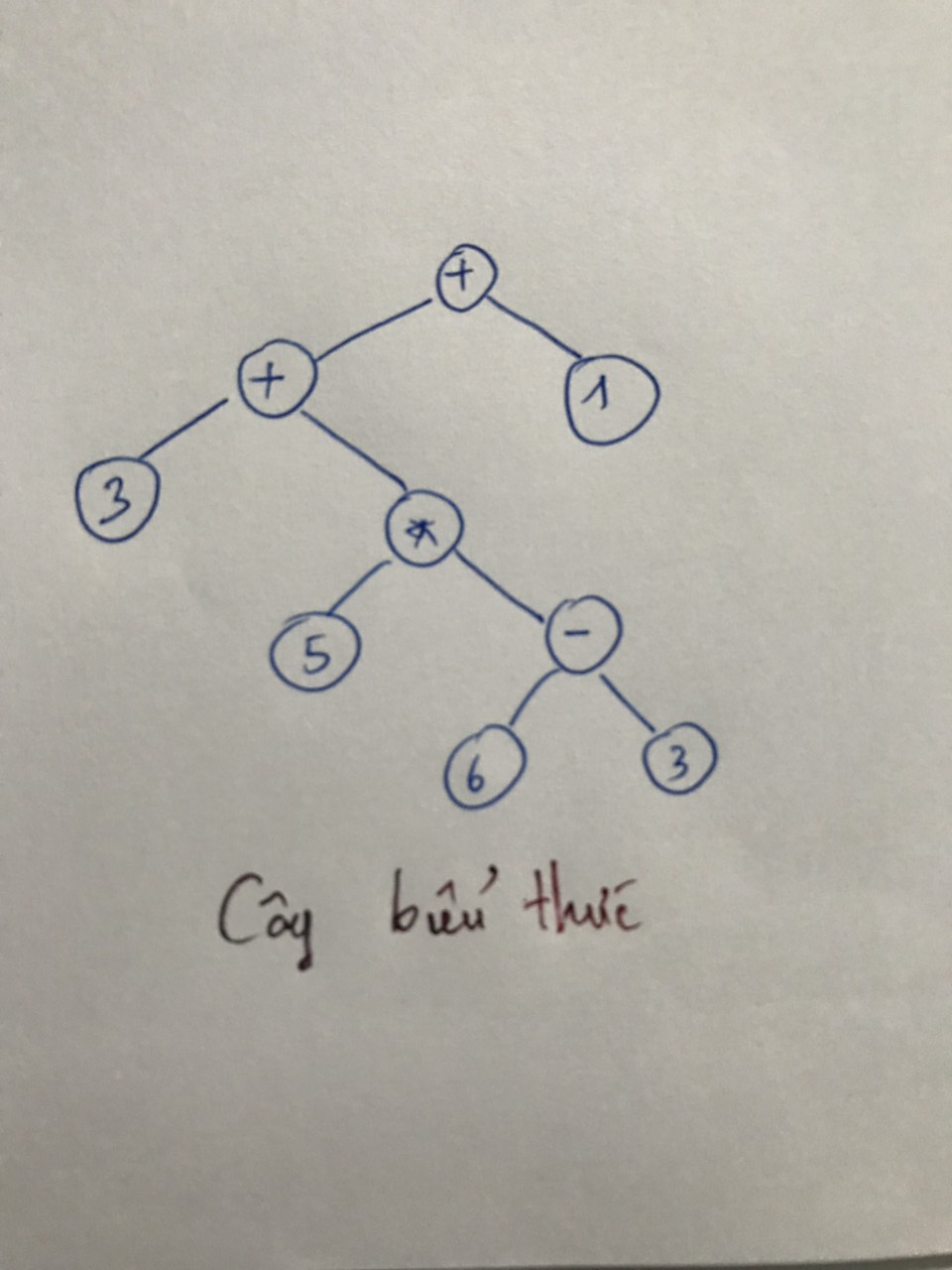
Đặc điểm của cây biểu thức:

• Tất cả các toán hạng (operand) đều nằm ở lá, các toán tử (operator) nằm ở các nodes khác lá
• Thứ tự duyệt
  • Duyệt giữa (lRr): Biểu thức tự nhiên
  • Duyệt trước (Rlr): Balan
  • Duyệt sau (lrR): Balan ngược.

II. Áp dụng kí pháp Balan trong calculator? (Application of Polish Notation)

Bài toán: Từ một chuỗi S = “$ 3+5*(6-3)+1 $”, viết chương trình để máy tính thực hiện.
Ở đây mình dùng Balan ngược:

1. Biểu diễn chuỗi S về kí pháp Ba lan ngược

Đây, kết quả mong muốn: $3\ 5\ 6\ 3 - * + 1 +$
But, How to do that?
(Tạm thời chỉ làm $+-*/$), nếu muốn làm nhiều hơn thì viết hàm getPriority() là được)
Ý tưởng: Dùng thêm Stack toán tử, duyệt qua các kí tự của chuỗi S

• Nếu S[i] là toán hạng (số): Cho ra output
• Nếu S[i] là toán tử: xét S[i] vs stack.top()
  • Nếu S[i] $<=$ stack.top() thì pop() stack ra output cho tới khi S[i] > stack.top() or stack empty or stack.top()==’(’
  • Nếu S[i] > stack.top() thì push vào stack
• Trường hợp S[i]=’(’ thì ta push vào Stack, S[i]=’)’ thì ta cứ pop() cho tới khi pop() luôn thằng ‘(’

2. Tính toán:

Từ chuối Balan ngược: RPN = $3\ 5\ 6\ 3 - * + 1 +$
Ý tưởng:

• Dùng 1 cái stack tính toán
• Duỵệt qua cái chuỗi balan ngược, nếu RPN[i] là toán hạng thì push vào stack, nếu là toán tử thì pop từ stack ra 2 thằng.
  • $ b= stack.top() $
  • $ a= stack. kề top() $

rồi lấy $a RPN[i] b$ và push kết quả đó vào lại stack. Kết quả cuối cùng là phần tử duy nhất còn lại trong stack.

Finally, Take your hand dirty, please!!!
Implement (please Take your hand dirty!!!)
Link code tham khảo