Segment Tree

December 28, 2019 5 minutes read

Segment Tree

28/12/2019

I. Mục đích:

Giúp truy xuất giá trị trên 1 đoạn (segment) nhanh chóng và update giá trị nhanh chóng. Nhanh ở đây là $O(log\ n)$. Truy xuất ở đây có thể là tổng, phần tử nhỏ nhất, phần tử lớn nhất, … .

II. Cấu tạo chung của 1 segment tree

Xét một array $a[n]$ (từ $0..n-1$), ta build $1$ cái cây quản lý mảng a.
Nói là cây nhưng thực chất là mảng: $Tree[4n]$.
Tại sao lại $4n$?
Đầu tiên ta xét vai trò của mỗi node trong Tree[]

$Node[1]$: root quản lý toàn bộ array, range $[0..n-1]$
$Node[2]$: quản lý range $[0..(n-1)/2]$
$Node[3]$: quản lý range $[(n-1)/2+1..n-1]$
$Node[4]$: …

Xét ví dụ minh họa sau sẽ rõ. 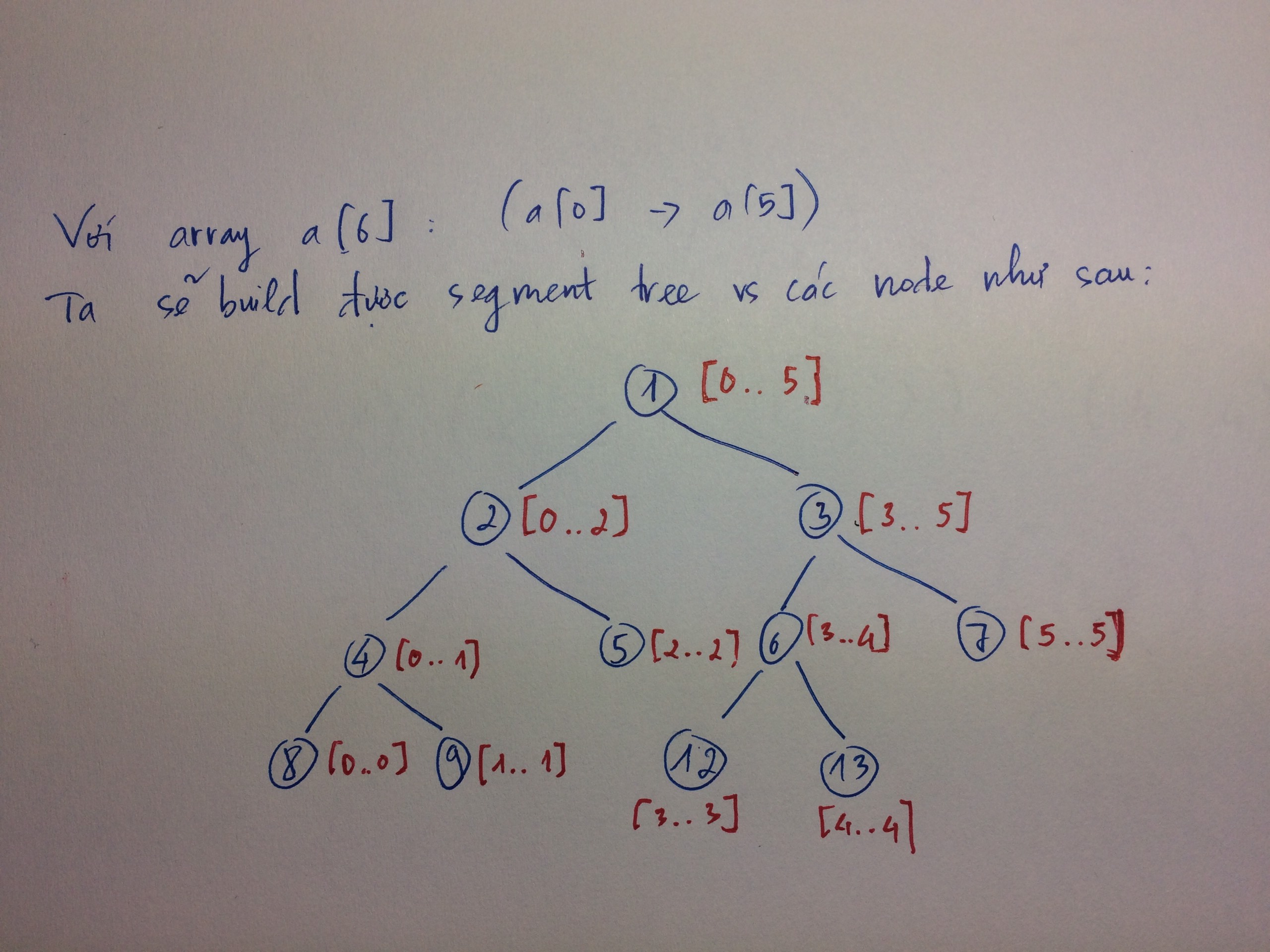Tree phải có $size = 4n$ vì như ta thấy với $n = 6$, thì nó cần tới node $13$ để quản lý tức $Tree[13]$ vì vậy $2n$ sẽ không đủ, mặc dù node $10$, $11$ (Tức $Tree[10]$, $Tree[11]$) chỉ là những dummy node. Có nghĩa là segment tree sẽ là $1$ cây nhị phân không đầy đủ, và để thêm đầy đủ thì tổng số node của nó sẽ là $T$.
$$ T = 2^0 + 2^1 + 2^2 + … + 2^m$$ với $ m = ceil\{log_2(n)\} \leq log_2(n) + 1$ $$\Rightarrow T = 2^0 + 2^1 + … + 2^{log_2(n)+1} = 2^{log_2(n)+2}-1 \leq 4n $$

III. Cài đặt Segment Tree thuần túy có Lazy Propagation.

 1//Khai báo dữ liệu
 2int n, a[N];
 3int Tree[4*N], Lazy[4*N];
 4//1. Hàm build cây từ a[n]
 5void build(int node, int st, int en) {
 6    if (st == en) {
 7        Tree[node] = a[st];
 8        return;
 9    }
10    build(2*node, st, (st+en)/2);
11    build(2*node+1, (st+en)/2+1, en);
12    Tree[node] = Tree[2*node] + Tree[2*node+1];
13}
14//2. Hàm get giá trị từ range [L..R]
15int get(int node, int st, int en, int L, int R){
16    // Nếu node hiện hành chưa update thì update đi rồi tính tiếp
17    if (Lazy[node]){
18        Tree[node] += (en - st + 1)*Lazy[node];
19        if (st != en) {
20            Lazy[2*node] += Lazy[node];
21            Lazy[2*node+1] += Lazy[node];
22        }
23        Lazy[node] = 0;
24    }
25    // 2 base case
26    if (en < L || st > R) return 0;
27    if (st >= L && en <= R) return Tree[node];
28    //case partial intersection
29    int p1 = get(2*node, st, (st+en)/2, L, R);
30    int p2 = get(2*node+1, (st+en)/2+1, en, L, R);
31    return (p1+p2);
32}
33//3. Hàm update giá trị từ range [L..R] với value v
34void update(int node, int st, int en, int L, int R, int v){
35    if (Lazy[node]) {
36        Tree[node] += (en - st + 1)*Lazy[node];
37        if (st != en) {
38            Lazy[2*node] += Lazy[node];
39            Lazy[2*node+1] += Lazy[node];
40        }
41        Lazy[node] = 0;
42    }
43    if (en < L || st > R) return;
44    if (st >= L && en <= R) {
45        Tree[node] += (en - st + 1)*v;
46        if (st != en) {
47            Lazy[2*node] += v;
48            Lazy[2*node+1] += v;
49        }
50        return;
51    }
52    update(2*node, st, (st+en)/2, L, R, v);
53    update(2*node+1, (st+en)/2+1, en, L, R, v);
54    Tree[node] = Tree[2*node] + Tree[2*node+1];
55}

Lưu ý

Có $2$ base case

  + node i cover [st..en] nằm ngoài range[L..R]
  + node i cover [st..en] nằm trong range[L..R]

Còn trường hợp partial sẽ tiếp tục recursive để đưa về base case.

Không thể xảy ra $st > en$ bởi vì ta đi từ $0..n-1$ và luôn chia $2$ thì không bao giờ có chuyện đó xảy ra nên khỏi lo.
Trật tự phải là Update node lazy trước rồi làm gì làm sau bởi vì khi node đó đã được gọi thì chứng tỏ thằng cha nó đang chờ kết quả từ nó báo về đề update cho nên dù nó có trong inside, outside hay partial thì update rồi tính sau. (Trong phần comment của HackerEarth có đó).

IV. Trường hợp suy biến của Segment Tree

Đặc điểm

Query 1 range
Update 1 phần tử

Cài đặt: Thay vì build từ root đến lá như segment tree thuần túy ta sẽ build từ lá đến gốc, vẫn với size bất kì $n$.
Các node từ $n$ đến $2n-1$ là các node lá chứa các phần tử $a[0]$ đến $a[n-1]$ của mảng $a$. Từ đó đi lên node cha nó là nó/2 và node 1 luôn là root.

 1int n, a[N];
 2int Tree[2*N]; //only need 2n (n nhỏ thôi)
 3int get(int L, int R){
 4    int res = 0;
 5    L += n; R += n;
 6    while(L<=R){
 7        if (L&1) res += Tree[L++];
 8        if (R&1==0) res += Tree[R--];
 9        L /= 2; R /= 2;
10    }
11    return res;
12}
13int update(int pos, int v){
14    pos += n;
15    Tree[pos] += v;
16    for(int k=pos/2; k>=1; k/=2){
17        Tree[k] = Tree[2*k] + Tree[2*k+1];
18    }
19}
20//build 1 tree
21for(int i=0; i<n; i++) update(i, a[i]);

Lưu ý cài đặt

Node con trái luôn là vị trí chẵn, Node con phải luôn là vị trí lẻ. Như vậy, $1$ node $k$ sẽ có con trái là $2k$, con phải là $2k+1$. (Bất kì size $n$ nào, đọc link codeforces sẽ rõ)

Segment Tree

I. Mục đích:

II. Cấu tạo chung của 1 segment tree

III. Cài đặt Segment Tree thuần túy có Lazy Propagation.

IV. Trường hợp suy biến của Segment Tree

V. Tham khảo