Traverse a Tree Recursively and Iteratively
In this article, I’m going to represent the algorithm of traversing a tree in every orders in both recursive way and especially iterative way.
To put it simply, the iterative way, we will you stack (only 1 stack) to simulate the process.
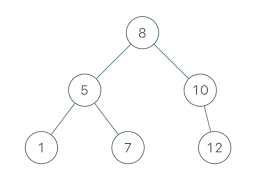
Assuming that the tree structure is as below:
1struct Node {
2 int value;
3 Node* left;
4 Node* right;
5 Node (int val) {
6 this->value = val;
7 this->left = this->right = NULL;
8 }
9};
1. Preorder Traversal
The preorder traversal goes through every node in the order: Root -> Left -> Right
So the desired result from above tree will be: 8->5->1->7->10->12
Recursive way:
The code is very popular and straight-forward
1void preorder(Node* root) {
2 if (root == NULL) return;
3 cout << root->value << "->";
4 preorder(root->left);
5 preorder(root->right);
6}
Iterative way:
The order of traversing is: Root -> Left -> Right
So how can we keep track of right & left node to get back later
The answer is put it in a stack
1void iterative_preorder(Node* root) {
2 stack<Node*> st;
3 st.push(root);
4 while(!st.empty()) {
5 Node* cur = st.top(); st.pop();
6 if (cur->right) st.push(cur->right);
7 if (cur->left) st.push(cur->left);
8 cout << cur->value << "->";
9 }
10}
2. Inorder Traversal
Order: Left -> Root -> Right
Recursive way
1void inorder(Node* root) {
2 if (root == NULL) return;
3 inorder(root->left);
4 cout << root->value << "->";
5 inorder(root->right);
6}
Iterative way
just like the approach post order using
1void iterative_inorder(Node* root) {
2 stack<Node*> st;
3 Node* cur = root;
4 while(cur || !st.empty()) {
5 if (cur) {
6 st.push(cur);
7 cur = cur->left;
8 } else {
9 cur = st.top(); st.pop();
10 cout << cur->value << "->";
11 cur = cur->right;
12 }
13 }
14}
3. Postorder Traversal
Order: Left -> Right -> Root
Recursive way
1void postorder(Node* root) {
2 if (root == NULL) return;
3 postorder(root->left);
4 postorder(root->right);
5 cout << root->value << "->";
6}
Iterative way
First, we examine the 2-stack approach, it’s very easy 1 stack used for traversal 1 stack used for storing answer, notice that we pop this stack to print the answer, so it will be push reversely
1void iterative_postorder_2_stacks(Node* root) {
2 stack<Node*> in;
3 stack<int> out;
4 in.push(root);
5 while(!in.empty()) {
6 Node* cur = in.top(); in.pop();
7 out.push(cur->value);
8 if (cur->left) in.push(cur->left);
9 if (cur->right) in.push(cur->right);
10 }
11 while(!out.empty()) {
12 cout << out.top() << "->";
13 out.pop();
14 }
15}
16
Let’s improve by using only 1 stack
1void iterative_postorder_1_stack(Node* root) {
2 stack<Node*> st;
3 Node* cur = root;
4 Node* prev = NULL;
5 while(cur || !st.empty()) {
6 if (cur) {
7 st.push(cur);
8 cur = cur->left;
9 } else {
10 cur = st.top();
11 if (cur->right == NULL || cur->right == prev) {
12 cout << cur->value << "->";
13 st.pop();
14 prev = cur;
15 cur = NULL;
16 } else { //right node hasn't handled yet
17 cur = cur->right;
18 }
19 }
20 }
21}
Code demo for all: link